Diferencia entre revisiones de «Definición de interbloqueo»
| Línea 10: | Línea 10: | ||
Según [http://es.wikipedia.org/wiki/Edsger_Dijkstra Dijkstra], una configuración de procesos y recursos es '''estado seguro''' si a partir de ella podemos seguir ejecutando código, es decir, no se producen interbloqueos. | Según [http://es.wikipedia.org/wiki/Edsger_Dijkstra Dijkstra], una configuración de procesos y recursos es '''estado seguro''' si a partir de ella podemos seguir ejecutando código, es decir, no se producen interbloqueos. | ||
| + | |||
| + | |||
| + | '''Ejemplo:''' Dados los procesos P1 y P2, su código es el siguiente. | ||
| + | |||
| + | <pre>P1 P2 | ||
| + | -- -- | ||
| + | |||
| + | while(1){ while(1){ | ||
| + | down(x); down(y); | ||
| + | acceso recurso_x(); acceso_recurso_y(); | ||
| + | down(y); down(x); | ||
| + | acceso_recurso_y(); acceso_recurso_x(); | ||
| + | up(y); up(x); | ||
| + | up(x); up(x); | ||
| + | } } | ||
| + | </pre> | ||
| + | |||
| + | Cronograma para los siguientes valores según planificación Round Robin: | ||
| + | |||
| + | q=3; | ||
| + | x=1; | ||
| + | y=1 | ||
| + | |||
| + | <pre> | ||
| + | X = El proceso pasa a estado bloqueado. | ||
| + | / = El proceso pasa a estado preparado. | ||
| + | > = Fin de su ejecución | ||
| + | </pre> | ||
| + | <pre> | ||
| + | | #1| #2| #3| | | | #4| | | ||
| + | P1|---|---|---| | | |---X | | ||
| + | | | | | | | | | | | ||
| + | | | | | #1| #2| #3| | #4| | ||
| + | P2| | | |---|---|---| |---X | ||
| + | | | | | | | | | | | ||
| + | |___|___|___|___|___|___|___|___| | ||
| + | 0 1 2 3 4 5 6 7 8 | ||
| + | </pre> | ||
| + | |||
| + | q=4; | ||
| + | x=1; | ||
| + | y=1 | ||
| + | |||
| + | <pre> | ||
| + | | #1| #2| #3| #4| | | #5| #6| #7| #1| | | | | #2| #3| #4| / | | | ||
| + | P1|---|---|---|---/ | |---|---|---|---/ | | | |---|---|---X | | | | ||
| + | | | | | | | | | | | | | | | | | | | | | | | ||
| + | | | | | | #1| #2| | | | | #3| #4| #5| #6| | | | #7| #1| #2| | ||
| + | P2| | | | |---|---X | / | |---|---|---|---/ | | |---|---|---X | ||
| + | | | | | | | | | | | | | | | | | | | | | | | ||
| + | |___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___| | ||
| + | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | ||
| + | </pre> | ||
| + | --[[Usuario:Leoberbue|Leoberbue]] ([[Usuario discusión:Leoberbue|discusión]]) 16:50 25 nov 2014 (CET) | ||
Revisión del 16:50 25 nov 2014
También conocido como bloqueo mutuo o deadlock.
Es una espera circular permanente de dos o más procesos. Existen una serie de condiciones para que se produzca y una serie de estrategias para resolverlos.
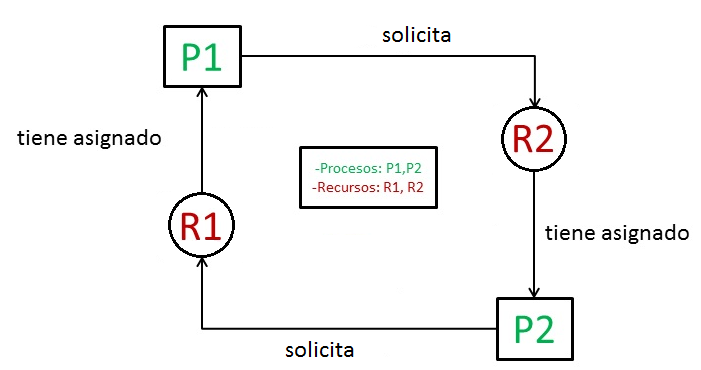
- Ejemplo simple:
Se aprecian dos procesos (P1 y P2), cada uno con un recurso diferente asociado (R1 y R2). Llega un punto en el que el proceso P1 ha adquirido el recurso R1 y el proceso P2 ha adquirido el recurso R2 y cada proceso necesita el otro recurso. Este es el punto de interbloqueo.
Según Dijkstra, una configuración de procesos y recursos es estado seguro si a partir de ella podemos seguir ejecutando código, es decir, no se producen interbloqueos.
Ejemplo: Dados los procesos P1 y P2, su código es el siguiente.
P1 P2
-- --
while(1){ while(1){
down(x); down(y);
acceso recurso_x(); acceso_recurso_y();
down(y); down(x);
acceso_recurso_y(); acceso_recurso_x();
up(y); up(x);
up(x); up(x);
} }
Cronograma para los siguientes valores según planificación Round Robin:
q=3; x=1; y=1
X = El proceso pasa a estado bloqueado.
/ = El proceso pasa a estado preparado.
> = Fin de su ejecución
| #1| #2| #3| | | | #4| |
P1|---|---|---| | | |---X |
| | | | | | | | |
| | | | #1| #2| #3| | #4|
P2| | | |---|---|---| |---X
| | | | | | | | |
|___|___|___|___|___|___|___|___|
0 1 2 3 4 5 6 7 8
q=4; x=1; y=1
| #1| #2| #3| #4| | | #5| #6| #7| #1| | | | | #2| #3| #4| / | |
P1|---|---|---|---/ | |---|---|---|---/ | | | |---|---|---X | | |
| | | | | | | | | | | | | | | | | | | | |
| | | | | #1| #2| | | | | #3| #4| #5| #6| | | | #7| #1| #2|
P2| | | | |---|---X | / | |---|---|---|---/ | | |---|---|---X
| | | | | | | | | | | | | | | | | | | | |
|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|___|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20