Diferencia entre revisiones de «Ejercicios»
De Wiki de Sistemas Operativos
(→Ejercicio 2) |
(→Ejercicio 1) |
||
| (No se muestran 6 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
= Ejercicio 1 = | = Ejercicio 1 = | ||
| − | Dada la siguiente configuración de procesos y recursos,elabore si la configuración es estado seguro. | + | Dada la siguiente configuración de procesos y recursos, elabore si la configuración es estado seguro. |
| Línea 9: | Línea 9: | ||
<tr> | <tr> | ||
| − | <td> </td> <td colspan="3">Adjudicados</td> <td colspan="3">Máximos</td> | + | <td> </td> <td colspan="3">Adjudicados</td> <td colspan="3">(M) Máximos</td> |
</tr> | </tr> | ||
| Línea 39: | Línea 39: | ||
[[Solución Ejercicio 1|Ver solución del ejercicio 1]] | [[Solución Ejercicio 1|Ver solución del ejercicio 1]] | ||
| − | = Ejercicio 2 = | + | = Ejercicio 2 = |
| + | |||
| + | Dada la siguiente configuración de procesos y recursos, elabore si la configuración es estado seguro. | ||
| + | |||
| + | <table BORDER="1" cellpadding="8"> | ||
| + | |||
| + | |||
| + | <tr> | ||
| + | <td> </td> <td colspan="3">Adjudicados</td> <td colspan="3">Z (Necesarios)</td> | ||
| + | </tr> | ||
| + | |||
| + | <tr> | ||
| + | <td> </td> <td>R1</td> <td>R2</td> <td>R3</td> <td>R1</td> <td>R2</td> <td>R3</td> | ||
| + | </tr> | ||
| + | |||
| + | <tr> | ||
| + | <td>P1</td> <td>3</td> <td>0</td> <td>2</td> <td>0</td> <td>2</td> <td>0</td> | ||
| + | </tr> | ||
| + | |||
| + | |||
| + | <tr> | ||
| + | <td>P2</td> <td>0</td> <td>2</td> <td>1</td> <td>1</td> <td>0</td> <td>0</td> | ||
| + | </tr> | ||
| + | |||
| + | |||
| + | <tr> | ||
| + | <td>P3</td> <td>1</td> <td>0</td> <td>0</td> <td>0</td> <td>0</td> <td>1</td> | ||
| + | </tr> | ||
| + | |||
| + | </table> | ||
| + | |||
| + | |||
| + | Disponibles = [ 1 1 0 ] | ||
| + | |||
| + | [[Solución Ejercicio 2 - Tema 8]] | ||
| + | |||
| + | = Ejercicio 3 = | ||
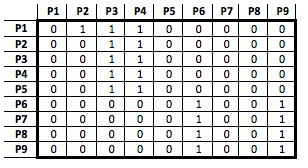
En un sistema en el que se ejecutan 9 procesos se usan matrices binarias de relación para detectar interbloqueos. En un momento dado, se calcula el cierre transitivo de la matriz T = WxA obteniendo como resultado la siguiente matriz: | En un sistema en el que se ejecutan 9 procesos se usan matrices binarias de relación para detectar interbloqueos. En un momento dado, se calcula el cierre transitivo de la matriz T = WxA obteniendo como resultado la siguiente matriz: | ||
| − | + | [[Archivo:Matriz_binaria_de_relaci_T.png]] | |
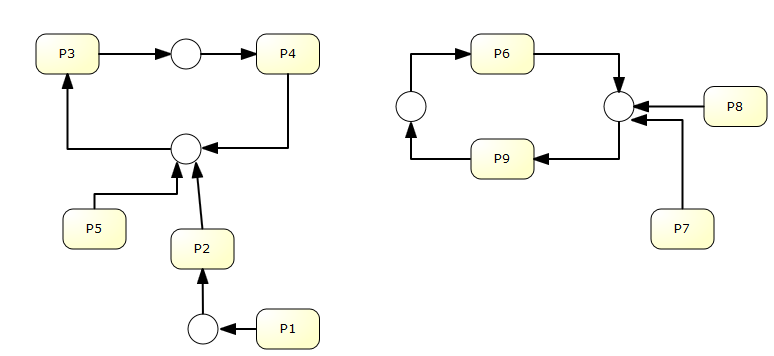
Exprese mediante grafos de relación proceso/recurso las posibles relaciones de espera entre los procesos del sistema. Represente los recursos sin nombre. | Exprese mediante grafos de relación proceso/recurso las posibles relaciones de espera entre los procesos del sistema. Represente los recursos sin nombre. | ||
[[Archivo:SoluciónEjercicio2.png]] | [[Archivo:SoluciónEjercicio2.png]] | ||
Revisión actual del 19:05 24 nov 2017
Ejercicio 1
Dada la siguiente configuración de procesos y recursos, elabore si la configuración es estado seguro.
| Adjudicados | (M) Máximos | |||||
| R1 | R2 | R3 | R1 | R2 | R3 | |
| P1 | 1 | 1 | 0 | 1 | 1 | 2 |
| P2 | 0 | 0 | 1 | 0 | 1 | 1 |
| P3 | 1 | 1 | 0 | 1 | 1 | 1 |
Disponibles = [ 1 0 1 ]
(Nota: Recordar que M = A+Z)
Ejercicio 2
Dada la siguiente configuración de procesos y recursos, elabore si la configuración es estado seguro.
| Adjudicados | Z (Necesarios) | |||||
| R1 | R2 | R3 | R1 | R2 | R3 | |
| P1 | 3 | 0 | 2 | 0 | 2 | 0 |
| P2 | 0 | 2 | 1 | 1 | 0 | 0 |
| P3 | 1 | 0 | 0 | 0 | 0 | 1 |
Disponibles = [ 1 1 0 ]
Ejercicio 3
En un sistema en el que se ejecutan 9 procesos se usan matrices binarias de relación para detectar interbloqueos. En un momento dado, se calcula el cierre transitivo de la matriz T = WxA obteniendo como resultado la siguiente matriz:
Exprese mediante grafos de relación proceso/recurso las posibles relaciones de espera entre los procesos del sistema. Represente los recursos sin nombre.